【智能学辅导教育集团】高中数学太难学不会？那是因为你还不“懂”数学！数学--这门学科，绝不只是加减乘除等的数字运算，它有内涵有思想，要想学好数学，首先你要“懂”它！

函数与方程思想

函数在高考中占比60%左右，所以函数可以说是高考的魂，高考的根基。函数思想是对于函数内容在更高层次上的抽象、概括与提炼，在研究数列、不等式、解析几何等方面有很重要的作用；那方程思想是解决各种计算问题的基本思想，是基本运算能力的必备。

什么是函数与方程思想？看例题：

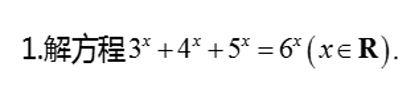
用我们现有的知识，无法直接求解，也就只能带入几个常数试验一下看看能不能恰好得到一个解，但是这也是没有办法写过程的。所以必须用数学的思想方法转化成我们熟悉的方程问题。首先考虑左右两边都存在指数函数，先化简一下，右边变为常数，左边变为可以用函数思想的部分。

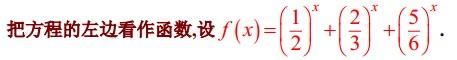
从这个函数上可以看出，f(x)是单调递减，进而通过验证法可以求解出x=3即为所求的解。所以只需一步，题目就转化为了熟悉的函数问题。

数形结合思想

数形结合思想就是把问题的数量关系和图形结合起来考查的思想方法，即根据解决问题的需要，可以把数量关系的问题转化为图形的性质和特征去研究，或者把图形的性质问题转化为数量关系的问题去研究。这个思想从初中就开始使用，到高中是升华和爆发。

数形结合思想的应用主要体现在三个方面：

(1)数转化为形，即根据的“数”的特点，构造符合条件的几何图形，用几何方法解决。

(2)形转化为数，即根据题目特点，用代数方法去研究几何问题。

(3)数形结合，即用数研究形，用形研究数，相互结合，使问题变得简捷、直观、明了。

数形结合的应用最深的印象应该是在直线与圆的章节，比如：

这些思路都将数学计算的问题转化为了图形问题。当然数形结合思想应用不仅仅局限于这些，它也活跃在函数、立体几何、圆锥曲线等知识中。

分类与整合思想

分类与整合思想，是一种重要的数学思想，也是一种重要的解题策略。它可以将整体化为局部，将复杂问题化为单一问题，以便于“各个击破”。但做题中要注意克服思维定势，处理好“分”与“合”，“局部”与“整体”之间的辩证统一关系，充分挖掘求解问题中潜在的特殊性与简单性，尽可能地简化或避免分类讨论。

一般，分类讨论主要是以下几个方面：

(1)所涉及的数学概念是分类进行定义的。

如|a|的定义分a>0、a＝0、a<0三种情况。这种分类讨论题型可以称为概念型。

(2)涉及的数学定理、公式和运算性质、法则有范围或者条件限制，或者是分类给出的。

如等比数列的前n项和的公式，分q＝1和q≠1两种情况，可以称为性质型。

(3)解含有参数的题目时，必须根据参数的不同取值范围进行讨论。

如解不等式ax>2时分a>0、a＝0和a<0三种情况讨论。这称为含参型。

(4)某些不确定的数量、不确定的图形的形状或位置、不确定的结论等，都主要通过分类讨论，保证其完整性，使之具有确定性。

化归与转化

这个思想主要是想将复杂问题化归为简单问题，将较难问题化为较易问题，将未解决问题化归为已解决问题。跟数形结合思想有点点类似，但是这个方法更具有灵活性和多样性，没有统一的模式，需要大家去寻找有利于问题解决的变换途径与方法。

经常用的几个转化的思路总结如下：

（1）立体几何问题，通常要转化